Question

mr. Martin's math class math test which is worth a hundred points has 29 problems each problems is worth either five points or two points let X be the number of questions worth 5 Points and let y be the number of questions worth two points x + y equals 29 5x + 2 y equals 100 how many problems of each point value are on the test

Answer 1

Let x be the number of questions worth 5 points and y be the number of questions worth 2 points.

`\begin{gathered} x+y=29\quad eq.1 \\ 5x+2y=100\quad eq.2 \end{gathered}`

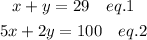
Let us solve this system of equations using the substitution method.

`\begin{gathered} x+y=29 \\ y=29-x\quad eq.1 \end{gathered}`

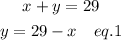
Substitute eq. 1 into eq. 2

`\begin{gathered} 5x+2y=100\quad eq.2 \\ 5x+2(29-x)=100 \\ 5x+58-2x=100 \\ 5x-2x=100-58 \\ 3x=42 \\ x=(42)/(3) \\ x=14 \end{gathered}`

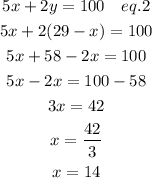
So, there are 14 questions worth 5 points.

Now substitute the value of x into eq. 1 to get the value of y

`\begin{gathered} y=29-x\quad eq.1 \\ y=29-14 \\ y=15 \end{gathered}`

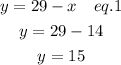
So, there are 15 questions worth 2 points.

Therefore, the correct answer is

14 questions worth 5 points and 15 questions worth 2 points.