Question

I stumbled upon a question I couldn’t answer, could you help me out?

Answer 1

Given,

The latent heat of vaporization of water, L=2.26×10⁶ J/kg

The specific heat capacity of the water, c=4190 J/kg/K

The density of the water, ρ=1000 kg/m³

The volume of the water, V=100 m³

The initial temperature of the water, T₁=18 °C

The final temperature of the water, T₂=100 °C

The mass of the given volume of water is,

`\begin{gathered} m=\rho V \\ =1000*100 \\ =100*10^3\text{ kg} \end{gathered}`

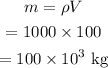
The heat needed to raise the temperature of the water to 100 °C is given by,

`Q_1=mc(T_2-T_1)`

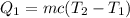
The heat needed to vaporize the water at 100 °C is given by,

`Q_2=mL`

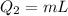
Thus the total heat energy needed is given by,

`\begin{gathered} Q=Q_1+Q_2 \\ =m\lbrack c(T_2-T_1)+L\rbrack \end{gathered}`

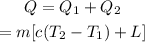
On substituting the known values,

`\begin{gathered} Q=100*10^3\lbrack4190(100-18)+2.26*10^6\rbrack \\ =2.6*10^(11)\text{ J} \end{gathered}`

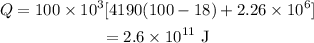
Thus the heat energy needed to evaporate the given amount of water is 2.6×10¹¹ J