Question

2. Determine the value of the variable in the figure below.ZW678 ft90 ftYX672 ft

Answer 1

Given:

ZY=90 ft, YX=672 ft, and ZX=678 ft.

WY=t

The line segment WY is perpendicular to the side ZX from the third vertex Z.

So WY is the altitude of the given triangle.

Let a=90 ft, b=672 ft and c=678 ft, and t is altutude.

The formula for the altitude is

`t=\frac{2\sqrt[]{s(s-a)(s-b)(s-c)}}{b}`

Here s is the semiperimeter of the tirangle .

`s=(a+b+c)/(2)`

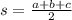
Substitute a=90ft, b=672, and c=678 in the equation , we get

`s=(90+672+678)/(2)=720\text{ ft}`

We get s=720ft.

Substitute s=720ft, a=90ft, b=672, and c=678 in the altitute formula, we get

`t=\frac{2\sqrt[]{720(720-90)(720-672)(720-678)}}{672}`

`t=\frac{2\sqrt[]{720*630**48*42}}{672}`

`t=\frac{2\sqrt[]{914457600}}{672}=90`

Hence the value of the variable is 90 ft.