Question

The Jamaican bobsled team hit the breaks on their sled so that it decelerates at a uniform rate of 0.43m/s^2. How long does it take to stop if it travels 85m before coming to rest?

Answer 1

Given:

The sled decelerates with a uniform rate of: a = -0.43 m/s^2 (The negative sign indicates that the velocity of the sled is decreasing)

The sled covers a distance of 85 m before coming to rest.

To find:

The time sled takes to come to rest

Step-by-step explanation:

We make use of the following kinematic equation,

`v^2=u^2+2as`

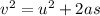
Here, v is the final velocity, u is the initial velocity, a is the deceleration and s is the displacement.

The final velocity v is zero as the sled is at rest. Thus, v = 0 m/s

The displacement of the sled after hitting the breaks is: s = 85 m

Substituting the values in the above equation, we get:

`\begin{gathered} 0=u^2-2*0.43\text{ m/s}^2*85\text{ m} \\ \\ u^2=73.1\text{ m}^2\text{/s}^2 \\ \\ u=\sqrt{73.1\text{ m}^2\text{/s}^2} \\ \\ u=8.55\text{ m/s} \end{gathered}`

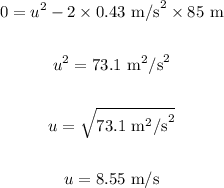
The initial velocity of the sled when breaks are applied is 8.55 m/s.

Now, consider another kinematical equation,

`v=u+at`

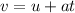
Substituting the values in the above equation, we get:

`\begin{gathered} 0=8.55\text{ m/s}-0.43\text{ m/s}^2* t \\ \\ t=\frac{8.55\text{ m/s}}{0.43\text{ m/s}^2} \\ \\ t=19.88\text{ s} \end{gathered}`

Final answer:

The sled takes 19.88 seconds before it comes to rest.