For A.
Bill's car
mass=900 kg
speed=3.5m/s towards west
Tanya's car
mass = 1100 kg
speed = 2 m/s towards East
The momentum

For P1 and P2
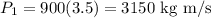
![P_2=1100(2)=2200\operatorname{kg}\text{ m/s}]()

then for the velocity, we have the final momentum
We can calculte the final momentum of Bill's
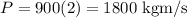
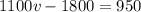
v is the velocity of Tanya’s car after the collision, so we need to isolate the v
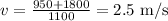
The velocity of Tanya's car after the collision is 2.5 m/s towards west
For B.
First, we need to calculate the kinetic energy before the collision of Bill's car and Tanya's car

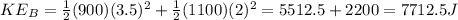
Then the kinetic energy after the collision

then
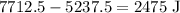
the energy that was converted to heat was 2475J