Question

The model for radioactive decay Is y = yor". A radioactive substance has a half-life of 60 years. Ir 100 grams are present today, in how many years will 68 es artis bepresent? While solving this problem, round the value of k to seven decimal places. Round your answer to two decimal places.KeypadAnswerHow to enter your answer opens in new windowadhat

Answer 1

We are given that the radioactive decay of a substance is given by the following equation:

`y=y_0e^(kt)`

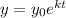
We need to determine the value of "k". To do that we will use the fact that the half-life of the quantity is 60 years. The half-life is the time for the quantity to be half the initial value, therefore, we have:

`(y_0)/(2)=y_0e^(k(60))`

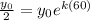
We can cancel out the initial quantity:

`(1)/(2)=e^(k(60))`

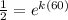
Now, we take the natural logarithm to both sides:

`ln((1)/(2))=ln(e^(k(60)))`

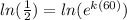
Now, we use the following property of logarithms:

`ln(x^y)=ylnx`

Applying the property we get:

`ln((1)/(2))=k(60)lne`

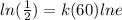
We also have:

`lne=1`

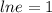
Substituting we get:

`ln((1)/(2))=k(60)`

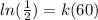
Now, we divide both sides by 60:

`(1)/(60)ln((1)/(2))=k`

Now, we solve the operations:

`-0.011552=k`

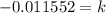
Now, we substitute the value of "k":

`y=y_0e^(-0.011552t)`

We are given that 100 grams is present today. If today is the value when time "t" is zero then 100 grams is the initial quantity, therefore, we substitute:

`y=100e^(-0.011552t)`

Now, we are asked to determine the time when "y = 68g":

`68=100e^(-0.011552t)`

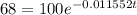
Now, we solve for "t". First, we divide both sides by 100:

`(68)/(100)=e^(-0.011552t)`

Now, we take the natural logarithm:

`ln((68)/(100))=lne^(-0.011552t)`

Now, we apply the property of logarithms:

`ln((68)/(100))=-0.011552tln(e)`

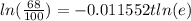
Applying "ln (e) = 1";

`ln((68)/(100))=-0.011552t`

Now, we divide both sides by -0.011552:

`-(1)/(0.011552)ln((68)/(100))=t`

Solving the operation:

`33.38=t`

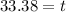
Therefore, the time required is 33.38 years.