Question

error analysis: describe and correct the error in solving the equation. 1) the only solution of the equation x^2+6x+9=0 is x=9

Answer 1

`x^2-8x-9=0\rightarrow\text{ Error-free equation}`

Step-by-step explanation: The only solution to the equation is x =9, we need to see if we can fix our equation such that the solution is indeed x = 9:

`\begin{gathered} x^2+6x+9=0\rightarrow\cdot(1)_{} \\ \end{gathered}`

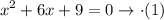
Plugging in x = 9 gives us:

`\begin{gathered} (9)^2+6(9)+9=0\rightarrow81+54+9=0 \\ 81+63=0\rightarrow\text{ False} \\ \therefore\rightarrow \\ 144\\e0 \end{gathered}`

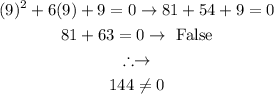
Fixing (1) gives us:

`\begin{gathered} x^2-8x-9=0\rightarrow(2)^{}^{} \\ \therefore\rightarrow \\ (9)^2-8(9)-9=0 \\ \therefore\rightarrow \\ 81--72-9=0\rightarrow81-81=0 \\ \therefore\rightarrow \\ 81-81=0\rightarrow\text{ True} \\ \end{gathered}`

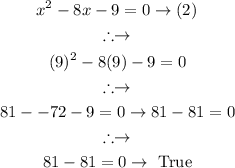
Therefore (2) is the new error-free equation, and the error is corrected by replacing + to - as a sign and replacing a coefficient.