Similar triangles have the same ratio between corresponding sides:
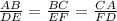
We have the sizes of the sides:
• AB = 17
,
• BC = 22
,
• CA = 2x-7
,
• DE = 34
,
• EF = 44
,
• FD = 2x+4
We use the ratio property to find x:
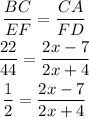
And now we clear x:
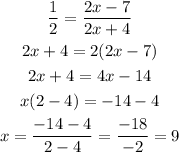
Now that we have x = 9, we can find the lenght of side DF (DF and FD are the same side):
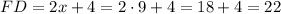
The answer is option C, FD = 22