Question

If MK = 10 m, find the length of MKL. Round to the nearest hundredth.o52KNMarc MKL =m

Answer 1

The measure of the central angle is equal to the measure of its subtended arc.

Since the central angle, JNL is subtended by the arc JKL

Then the measure of arc JKL = the measure of angle JNL

Since the measure of angle JNL = 90 degrees, then

The measure of arc JKL = 90 degrees

Since the measure of arc JKL = m of arc JK + m of arc KL, then

90 = 52 + m arc KL

Subtract 52 from both sides

90 - 52 = 52 - 52 + m arc KL

38 = m arc KL

Since the measure of the circle is 360 degrees

Since arc MK is half the circle because KM is a diameter, them

m of arc MKL = m arc MK + m arc KL

m of arc MKL = 180 + 38

m of arc MKL = 218

Now we will find its length using this rule

`L=(218)/(360)*2*\pi* r`

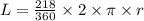
r is the radius of the circle

Since MK is the diameter o the circle, then

`r=(MK)/(2)=(10)/(2)=5`

Substitute it in the rule and use pi = 3.14

`\begin{gathered} L=(218)/(360)*2*3.14*5 \\ L=19.01444444 \end{gathered}`

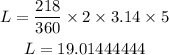
Round it to the nearest hundredth, then

L = 19.01 m or 19.02 if you use the value of pi on the calculator