Question

1 Drag the tiles to the correct boxes. Not all tiles will be used. Consider the exponential functions f g and h, defined as shown. function f function g function h YA h X g(x) -1 1 0 4 fx) = -2(3)X + 6 -2 11 16 2 اسم 2. 64 -2. 3 256 Determine which function or functions have each key feature.

Answer 1

We have three functions and we have to identify some properties.

1) x-intercept at (1,0).

This means that when y=0, x is 1.

We start by testing this with f(x):

`\begin{gathered} f(x)=0=-2(3)^x+6 \\ -6=-2\cdot3^x \\ (-6)/(-2)=3^x \\ 3=3^x \\ \ln (3)=x\cdot\ln (3) \\ 1=x \\ x=1 \end{gathered}`

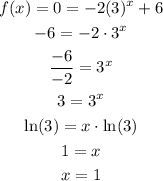
The function f(x) has the x-intercept at (1,0).

The table for g(x) shows us that when x=1, y=16 so it does not have a x-intercept at (1,0).

In th graph for h(x), we can see that the line intercepts the x-axis at point x=1, so the function has a x-intercept at (1,0)

Answer: f(x) and h(x)

2) Approaches an integer as x approaches minus infinity.

We can calculate this limit for f(x):

`\lim _(x\to-\infty)-2(3^x)+6=0+6=6`

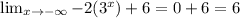
The funtion f(x) approaches an integer when x approaches minus infinity.

For g(x), we estimate that there is a common ratio of 4, so when x approaches minus infinity, the function approaches 0. then, g(x) also approaches an integer as x approaches minus infinity.

In the graph of h(x) can also be estimated that there is an horizontal assymptote when x approaches minus infinity, so h(x) also satisfies this condition.

Answer: all three functions.

3) Increasing on all intervals of x.

f(x) and h(x) decrease when x increases, so they don't satisfy this condition.

The function g(x) increases when x increases for all values of x, so it satisfies this condition.

Answer: g(x)

4) y-intercept at (0,4)

This can be calculated as the values of the functions when x=0.

For f(x) we have:

`f(0)=-2(3^0)+6=-2\cdot1+6=-2+6=4`

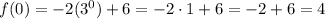
f(x) has the y-intercept at (0,4).

In the table, we can see that g(0)=4, so it also satisfies this condition.

The function h(x) intercepts the y-axis at (0,3) so it does not satisfy this condition.

Answer: f(x) and g(x)