Question

Equation match a.) m= -2/3, b=3b.) m = -3/2, (4,-1)

Answer 1

Given:

A.)

Slope of the line (m) = -2/3

Y-intercept (b) = 3

The given can be used to make an equation under the Slope-Intercept Form:

`\text{ y = mx + b}`

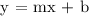
By substituting m and b to y = mx + b, we can generate the equation.

We get,

`\text{ y = mx + b}`
`\text{ y = (-2/3)x + (3)}`
`\text{ y = -}(2)/(3)x\text{ + 3}`
`3(\text{ y = -}(2)/(3)x\text{ + 3)}`
`3y\text{ = -2x + 9}`
`2x\text{ + 3y = 9}`

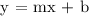
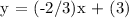
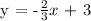
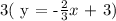
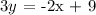
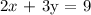
Therefore, the equation match to m = -2/3 and b = 3 is 2x + 3y = 9.

B.)

Slope of the line (m) = -3/2

x,y = 4,-1

To be able to generate the equation, let's first determine the y-intercept (b). We can get it by substituting m = -3/2 and x,y = 4,-1 to the equation y = mx + b.

We get,

`\text{ y = mx + b}`
`\text{ -1= (-3/2)(4) + b}`
`-1\text{ = }(-12)/(2)\text{ + b }\rightarrow\text{ -1 = -6 + b}`
`\text{ b = -1 + 6}`
`\text{ b = 5}`

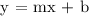
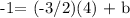
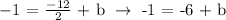
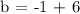
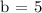
Since we now found that the y-intercept (b) = 5, let's substitute b and m = -3/2 to y = mx + b to generate the equation.

We get,

`\text{ y = mx + b}`
`\text{ y = (-3/2)x + (5)}`
`\text{ y = -}(3)/(2)x\text{ + 5}`
`\text{ -2(y = -}(3)/(2)x\text{ + 5)}`
`\text{ -2y = 3x - 10}`

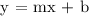
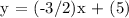
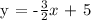
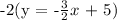
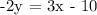
Therefore, the equation that match m = -3/2 and (4,-1) is -2y = 3x - 10.