If we draw a rectangle under the graph, we can find that the width w of the rectangle is 2x and the height h is 25 - x^2.
So, the area of the rectangle is,
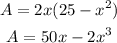
Differentiate the function to find maxiumum.
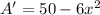
Putting A'=0,
![\begin{gathered} x^2=(50)/(6)=(25)/(3) \\ x=+\frac{5}{\sqrt[]{3}}or-\frac{5}{\sqrt[]{3}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7209kbjv763ajvxuwexkct583ack8mtco2.png)
x should be positive So,
![x=\frac{5}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/yrvvihxlw278cqui9z7qpjfoezpdyc0rn1.png)
Differentiate A' with respect to x to find if it is a maximum.
![\begin{gathered} A^(\doubleprime)=-12x<0 \\ \text{when x=}\frac{\text{5}}{\sqrt[]{3}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q10uwkvm7mi5m9y42u9ft1q2loh817nfqy.png)
It confirms that area is a maximum for x.
So, the width of the rectangle with largest area is ,
![w=2x=2*\frac{5}{\sqrt[]{3}}=\frac{10}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/2b9kon1hlrau44c2mf8umz2ezjkiailt14.png)
![\begin{gathered} h=25-x^2 \\ h=25-(\frac{5}{\sqrt[]{3}})^2 \\ h=25-(25)/(3) \\ h=(50)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8qmb4k1plwt0w9lunguh5t0c06vsnow59y.png)