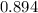Solution:
Let X be the number on each ball. The probability distribution is:
now, the mean is
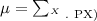
According to the data, this Mean would be:
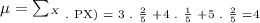
So, we get that the Mean is:
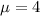
Now, the variance is
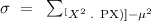
According to the data of the problem, we get that the variance is:
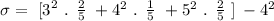
this is equivalent to:
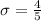
Thus, the standard deviation would be:
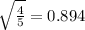
Then, we can conclude that the correct answer is:
Variance:
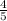
Standard deviation: