Question

Dylan is driving to a concert and needs to pay for parking. There is an automatic fee of $5 just to enter the parking lot, and when he leaves the lot, he will have to pay an additional $2 for every hour he had his car in the lot. How much total money would Dylan have to pay for parking if he left his car in the lot for 6 hours? How much would Dylan have to pay if he left his car in the lot for tt hours?Cost of parking for 6 hours: Cost of parking for tt hours:

Answer 1

Here, we have a fixed parking cost and a variable parking lot that is a function of the time spent in the lot. Our approach is to create an algebraic relationship and then slot in our variable vales to solve.

Let c represent the cost of parking.

Let t represent the time car spent in the lot.

We then have:

`c=5+2t`

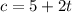
To calculate the cost of 6 hours in the lot, we have:

`\begin{gathered} c=5+2(6) \\ c=5+12=17 \end{gathered}`

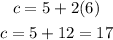
$17 for a 6 hour packing.

Cost for tt hours.

`c=5+2(tt)`

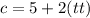
Cost for tt hours = c = 5+2(tt)