EXPLANATION
Let's see the facts:
The Area is 25.12cm^2
The Area of the circle is given by the following equation:

We need to isolate r in order to get the length of the side:
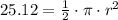
Dividing both sides by pi:
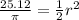
Multiplying both sides by 2:
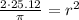
Now, we need to apply the square root to both sides:
![\sqrt[]{(2\cdot25.12)/(\pi)}=r](https://img.qammunity.org/2023/formulas/mathematics/college/m9nixune59wvfepbckvzjp560fdwrr4mj2.png)
Switching sides:
![r=\sqrt[]{(50.24)/(\pi)}=\sqrt[]{16}](https://img.qammunity.org/2023/formulas/mathematics/college/u3s8r1kvadu6fk88vbtw2lww8tebhollxt.png)
Simplifying the square root:
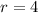
The radius is r=4, but the diameter of the semicircle is equivalent to the side of the square so,
Side of square = Diameter of semicircle = 2*4 = 8
The answer is 8cm