Question

The displacement-time graph below represents the motion of a cart initially moving forward along a straight line. During which interval is the cart accelerating?

Answer 1

The cart is accelerating during the interval AB.

This is because the slope of the displacement-time graph is increasing during this interval. A positive slope indicates that the cart is moving forward, and an increasing slope indicates that the cart is speeding up (i.e., accelerating).

During the interval CD, the slope of the displacement-time graph is constant. This indicates that the cart is moving forward at a constant speed.

Therefore, the answer is: AB

Answer 2

Interval AB

Step-by-step explanation

The horizontal displacement of an object is given by the equation,

`x=x_o+ut+(1)/(2)at^2`

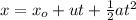
Where u is the initial velocity and a is the acceleration of the object.

Also, the velocity of the same object is given by,

`v=u+at`

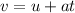
If the object is moving at a constant speed, it means that the speed does not change during its motion. According to the equation above, this means that for the speed to be constant there must be no acceleration - i.e. a = 0. In that case, the equation that models the displacement is,

`x=x_o+ut`

As we can see, this is a linear equation, unlike the first one written - which is a quadratic equation.

Similarly, if the object has no velocity - in other words, it is not moving, then the equation is a constant,

`x=x_o`

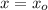
Now, with all this, we can analyze the graph. Note that the interval CD is a horizontal line, so it means that the displacement is constant and, therefore, there is no velocity and no acceleration either.

Segments BC and DE are straight lines, so they must be represented by a linear equation - like the one we found where the velocity was constant. Thus, for those two intervals, there is no acceleration.

Finally, interval AB shows a parabola - which is a quadratic equation, represented by the first equation we wrote.

Hence, the cart is accelerating during interval AB.