Rate of Change
As stated in the question, the rate of change measures how one quantity changes with respect to another.
The question talks about two quantities: The number of hours passed and the number of candies sold. The corresponding data is shown in the table.
Let's call H to the number of hours passed and C to the number of candies sold. We are interested in calculating the changes of C divided by the changes of H as follows:
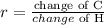
Take the first two rows of the table. The change of C is 9 - 5 = 4. The change of H is 8 - 7 = 1, thus the rate of change is:
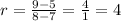
This means 4 candies are sold per hour.
Now take the second and the third rows.
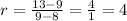
Again, we get 4 candies per hour.
You can use any pair of rows (including non-continuous rows) and you will get the same result.
Based on those results, we can conclude the rate of change is constant and has a value of 4 candies per hour.