Question

One hose can fill a small swimming pool in 70 minutes. A larger hose can fill the pool in 55 minutes. How long will it take the two hoses to fill the pool workingtogether?Do not do any rounding.

Answer 1

To determine the time it takes for the two hoses to fill the pool, we have the equation below:

`(1)/(70)+(1)/(55)=(1)/(t)`

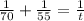
where t = time in minutes for the two hoses to fill the poll.

Let's add the fractions on the left side by applying the Butterfly Method.

`\begin{gathered} (1(55)+1(70))/(70(55))=(1)/(t) \\ (55+70)/(3850)=(1)/(t) \\ (125)/(3850)=(1)/(t) \end{gathered}`

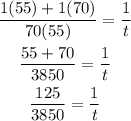
Then, let's cross multiply.

`125t=3850`

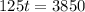
Lastly, divide both sides by 125.

`\begin{gathered} (125t)/(125)=(3850)/(125) \\ t=30.8\min \end{gathered}`

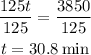
Hence, it will only take 30.8 minutes for the two hoses together to fill the pool.