The general equation of a line is given below as

The equation of the line given in the question is
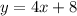
By comparing coefficients, we will have the value of the gradient to be
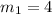
The coordinates of the second line given are
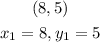
Two lines are perpendicular when the products of their gradients is equal to -1, that is
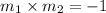
Substituting the value of m1, we will have
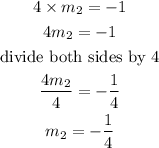
The formula to calculate the equation of a line when one point and the slope are given is
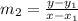
By substituting the values, we will have
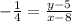
Cross multiply the equation above, we will have that
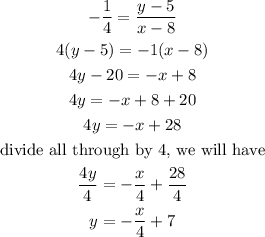
Hence,
The equation of the line perpendicular to y=4x+8 and passes through (8,5) =
y=-x/4 + 7