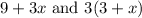The expressions we have are:

To find the correct answer, we have to use the distributive property on the options and check if the expressions are the same.
Let's analyze the options:
In option F we have:
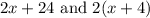
We need to use distributive property on the second expression and check if we get the same as in the first of the expressions.

Distributive property tells us to multiply the outside number by both of the terms inside the parenthesis:
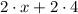
Solving the multiplications:
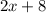
This is different from 2x+24, so the expressions are not equivalent.
In Option G we have:
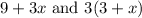
Using distributive property on the second expression:
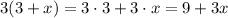
As we can see, the second expression is 9+3x, which is also the first expression, this means that the expressions are EQUIVALENT.
Answer: G