Question

19. Find the value of x to the nearest tenth. 6

Answer 1

In order to solve this, we can use trigonometric ratios. The cosine ratio is given by the following formula:

`\cos \theta=(ca)/(hy)`

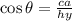
Where ca is the adjacent leg to angle θ and hy is the length of the hypotenuse. In this case, θ=50°, ca = 6 and hy = x.

By replacing these values into the above formula, we get:

`\cos 50=(6)/(x)`

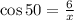
From this equation, we can solve for x to get:

`x=(6)/(\cos 50)=9.3`

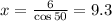
Then, x = 9.3