Given:
The amount after 10 years and 8 months, A=$750.00.
The rate of interest, r =2 1/2 %.
The period of time, t =10 years and 8 months.
The interest is compounded daily
Required:
We need to find the intial investment amount.
Step-by-step explanation:
Conver the period of time to years.
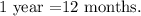
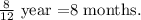


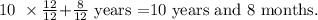
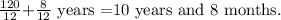
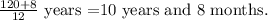

We get t =128/12.
The annual interest rate is
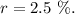
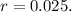
The number of days in a year = 365 days.
The money is compounded daily, n=365.
Consider the formula to find the amount in compound interest.

Substitute A =750, r=0.025, n=365 and t =128/12 in the formula.

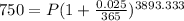
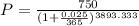
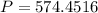
Final answer:
The initial amount is $ 574.45.