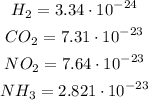Question

drag the tiles to the correct boxes to complete the pairs use this table to match the molecules with their estimated masses

Answer 1

Scientific notation

We want to add the indicated atoms mass for each tile

H₂: 2 atoms of hydrogen

Since each hydrogen atom's mass corresponds to

`1.67\cdot10^(-24)`

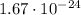
Then H₂:

`\begin{gathered} H_2=2\cdot H \\ H_2=2\cdot1.67\cdot10^(-24) \end{gathered}`

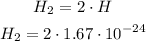
we multiply just the numbers without exponent:

`\begin{gathered} H_2=2\cdot1.67\cdot10^(-24) \\ =3.34\cdot10^(-24) \end{gathered}`

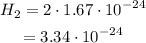
CO₂: 1 atom of carbon and 2 atoms of oxygen

Similarly, to the previous, we know that:

`\begin{gathered} CO_2=C+2\cdot O \\ CO_2=1.99\cdot10^(-23)+2\cdot2.66\cdot10^(-23) \end{gathered}`

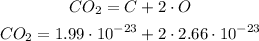
First we multiply the numbers without exponent: 2 * 2.66:

`\begin{gathered} 2\cdot2.66=5.32 \\ CO_2=1.99\cdot10^(-23)+5.32\cdot10^(-23) \end{gathered}`

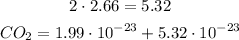
Now, we can add both terms:

`\begin{gathered} CO_2=1.99\cdot10^(-23)+5.32\cdot10^(-23) \\ CO_2=(1.99^{}+5.32)\cdot10^(-23) \\ CO_2=7.31\cdot10^(-23) \end{gathered}`

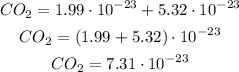
NO₂: 1 atom of nytrogen and 2 atoms of oxygen

We know that:

`\begin{gathered} NO_2=N+2\cdot O \\ NO_2=2.32\cdot10^(-23)+2\cdot2.66\cdot10^(-23) \end{gathered}`

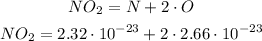
We can see this is really similar to the previous one.

We follow the same procedure:

First we multiply the numbers without exponent: 2 * 2.66:

`\begin{gathered} 2\cdot2.66=5.32 \\ NO_2=2.32\cdot10^(-23)+5.32\cdot10^(-23) \end{gathered}`

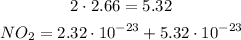
Now, we can add both terms:

`\begin{gathered} NO_2=2.32\cdot10^(-23)+5.32\cdot10^(-23) \\ NO_2=(2.32^{}+5.32)\cdot10^(-23) \\ NO_2=7.64\cdot10^(-23) \end{gathered}`

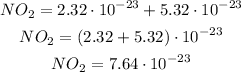
NH₃: 1 atom of nytrogen and 2 atoms of hydrogen

We know that:

`\begin{gathered} NH_3=N+3\cdot H \\ NH_3_{}=2.32\cdot10^(-23)+3\cdot1.67\cdot10^(-24) \end{gathered}`

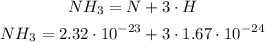
First we multiply the numbers without exponent: 3 * 1.67:

`\begin{gathered} 3\cdot1.67=5.01 \\ NH_3=2.32\cdot10^(-23)+5.01\cdot10^(-24) \end{gathered}`

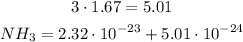
For the first time we have two terms with different 10 power:

on one side 10⁻²³ and on the other 10⁻²⁴

We want both have the same because if they are different we cannot add them.

Then we want to transform

5.01 · 10⁻²⁴

Into

___ · 10⁻²³

We need to find that number

Since

`10^(-1)\cdot10^(-23)=10^(-24)`

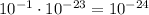
Then

`5.01\cdot10^(-1)\cdot10^(-23)=5.01\cdot10^(-24)`

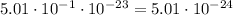
We know that

`\begin{gathered} 10^(-1)=(1)/(10)=0.1 \\ \downarrow \\ 5.01\cdot10^(-1)=5.01\cdot0.1=0.501 \end{gathered}`

Then

`5.01\cdot10^(-24)=5.01\cdot10^(-1)\cdot10^(-23)=0.501\cdot10^(-23)`

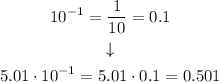
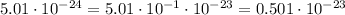
Then, getting back to our equation for NH₃, we have that:

`\begin{gathered} NH_3=2.32\cdot10^(-23)+5.01\cdot10^(-24) \\ NH_3=2.32\cdot10^(-23)+0.501\cdot10^(-23) \end{gathered}`

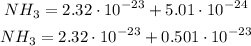
Now, we can add normally as we did on the previous molecules:

`\begin{gathered} NH_3=2.32\cdot10^(-23)+0.501\cdot10^(-23) \\ NH_3=(2.32+0.501)\cdot10^(-23) \\ NH_3=2.821\cdot10^(-23) \end{gathered}`

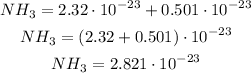
Answer:

`\begin{gathered} H_2=3.34\cdot10^(-24) \\ CO_2=7.31\cdot10^(-23) \\ NO_2=7.64\cdot10^(-23) \\ NH_3=2.821\cdot10^(-23) \end{gathered}`