Step-by-step explanation
To solve this problem, we will use:
(1) Pitagoras Theorem, which states for a right triangle:
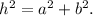
Where a and b are the cathetus, and h is the hypotenuse.
(2) The formula for the area of a triangle:
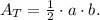
Where a is the height and b is the base.
(3) The formula for the area of a semi-circle:
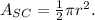
Where r is the radius and π ≅ 3.14.
(4) Length or perimeter of a semi-circle:
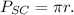
---------------------------------------------------
(b) From this figure, we identify:
0. a semicircle of radius r = 5 cm,
,
1. a right triangle with height a = 10 cm and hypotenuse h = √200 cm.
Using Pythagoras Theorem, we have:
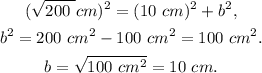
1) The area of the complete figure is the sum of the areas of the semi-circle and triangle:
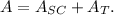
Using the formulas and values from above, we get:
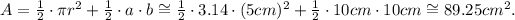
2) The perimeter of the figure is the sum of the length of the sides:
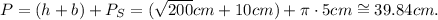
(c) From this figure, we identify:
0. a semi-circle with radius r₁ = 18 cm / 2 = 9 cm,
,
1. two semi-circles with radius r₂ = 9 cm / 2 = 4.5 cm.
1) The area of the figure is given by the sum of the areas of the semi-circles:
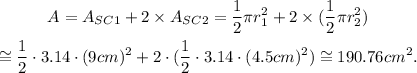
2) The perimeter of the figure is the sum of the perimeters of the semi-circles:
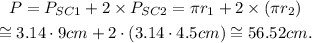
Answer
(b) Figure b
• Area ≅ 89.25 cm²
,
• Perimeter ≅ 39.84 cm
(c) Figure c
• Area ≅ 190.76 cm²
,
• Perimeter ≅ 56.52 cm