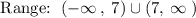Question

Identify the domain and range of the reciprocal function y=2/x+3 +7

Answer 1

`\begin{gathered} \text{ Domain: }\left(-\infty\:,\:-3\right)\cup\left(-3,\:\infty\:\right) \\ \\ \text{ Range: }\left(-\infty\:,\:7\right)\cup\left(7,\:\infty\:\right) \end{gathered}`

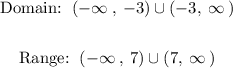
Explanation:

We have the following function:

`\:y=(2)/(x+3)\:+7`

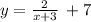
The domain is the input values of the function, in this case, it would be the interval of values that x can take, while the range is the output values of the function, that is, in this case, it would be the interval of values that it can take y.

In the case of a reciprocal function, the domain is affected since the denominator can never be 0 since it generates a mathematical indeterminacy, therefore, we calculate the domain by setting the denominator equal to 0, just like this:

`\begin{gathered} x+3=0 \\ \\ x=-3 \\ \\ \text{ therefore:} \\ \\ \text{Domain: }\left(-\infty\:,\:-3\right)\cup\left(-3,\:\infty\:\right) \end{gathered}`

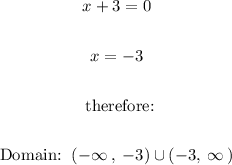
The range is affected by the fact that it can never be the value of 7, because the previous expression has no way of making it equal to 0, therefore the range would be:

`\text{ Range: }\left(-\infty\:,\:7\right)\cup\left(7,\:\infty\:\right)`