Question

A drone hovers at a position that is 100 m above ground level. It carries a bowling ball that can be released into freefall via a remote control. The bowling ball is released at t= 0 from rest. a) With what velocity would the bowling ball reach the ground if unobstructed? b) IF: At the same time the Bowling ball is released, a projectile is launched from ground level with an initial velocity of 35.0 m/s at 60.0° with respect to the horizontal. Which object would reach the ground first and by how much time? c) IF: At the same time the bowling ball is released the projectile is launched, at what time will they be at the same elevation relative to the ground? d) IF: The bowling ball is released at t=0, at what time before or after that should the projectile be launched such that the bowling ball collides with it when is reaches its maximum height? Assume that the drone is positioned directly above the location which the projectile will be when at its maximum height.

Answer 1

Given:

Height = 100 m

The bowling ball is released at t= 0 from rest.

Let's solve for the following:

• (a). With what velocity would the bowling ball reach the ground if unobstructed?

Apply the motion equation:

`v^2=u^2+2as`

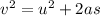
Where:

• v is the final velocity

,

• u is the initial velocity = 0 m/s

,

• a is acceleration due to gravity = 9.8 m/s²

,

• s is the height = 100 m

Substitute values into the formula and solve for v:

`\begin{gathered} v^2=0+2(9.8)(100) \\ \\ v^2=1960 \\ \\ \text{Take the square rooto of both sides:} \\ \sqrt[]{v^2}=\sqrt[]{1960} \\ \\ v=44.27\text{ m/s} \end{gathered}`

The velocity it would take the bowling ball to reach the ground is 44.27 m/s.

• (b). Given:

Initial velocity of projectile = 35.0 m/s

Angle = 60.0 degrees

Let's determine the object that would reach the ground first.

We have:

`\begin{gathered} T_{\text{projectile}}=(2u\sin\theta)/(g)=(2*35\sin60)/(9.8)=6.19\text{ seconds} \\ \\ T_{\text{ball}}=(44.27)/(9.8)=4.52\text{ seconds} \end{gathered}`

• It will take the projectile 6.19 seconds to reach the ground.

,

• It will take the ball 4.52 seconds to reach the ground.

Change in time = 6.19 - 4.52 = 1.67 seconds

Therefore, the ball will reach the ground first with 1.67 seconds less.

(c). To find the time both the ball and projectile will be at the same elevation relative to the ground, we have the equations:

`\begin{gathered} H_(ball)=100-(1)/(2)gt^2 \\ \\ H_(projectile)=(35\sin 60)t-(1)/(2)gt^2 \end{gathered}`

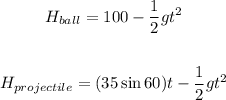
Eliminate the equal sides and equate the expressions on the left:

`\begin{gathered} 100-(1)/(2)gt^2=(35\sin 60)t-(1)/(2)gt^2 \\ \\ \text{Cancel co}mmon\text{ factors:} \\ 100=(35\sin 60)t \\ \\ t=(100)/(35\sin 60) \\ \\ t=(100)/(30.31) \\ \\ t=3.29\approx3.3\sec onds \end{gathered}`

Therefore, the time thwy will be at the same elevation relative to the ground is 3.29 seconds.

• (d).Apply the equations:

`T_(max)=(u\sin\theta)/(g)=(35\sin 60)/(9.8)=\text{3}.09\text{ seconds}`

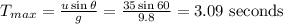
Now, take the equation for maximum height:

`\begin{gathered} H_(\max )=(u^2\sin ^2\theta)/(2g) \\ \\ H_(\max )=\frac{35^2(\sin 60)^2^{}}{2(9.8)}=46.88\text{ m} \end{gathered}`

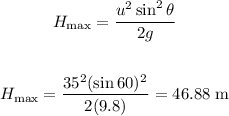
Hence the difference in height by the drone is:

100 m - 46.88 m = 53.12 m

To find the time , apply the formula:

`\begin{gathered} (1)/(2)gt^2=53.12 \\ \\ \end{gathered}`

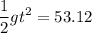
Rewrite the equation for t:

`\begin{gathered} t=\sqrt[]{(2*53.12)/(g)} \\ \\ t=\sqrt[]{(2*53.12)/(9.8)} \\ \\ t=3.29\text{ seconds} \end{gathered}`

ANSWER:

• (a). 44.27 m/s

,

• (b). The ball will reach the ground first with 1.67 seconds less.

,

• (c). 3.29 seconds

,

• (d) 3.29 seconds