Question

Only about 16% of all people can wiggle their ears. Is this percent different for millionaires? Of the 342 millionaires surveyed, 58 could wiggle their ears. What can be concluded at the α = 0.01 level of significance?For this study, we should use Select an answerThe null and alternative hypotheses would be: H0: ? Select an answer (please enter a decimal) H1: ? Select an answer (Please enter a decimal)The test statistic ? = (please show your answer to 3 decimal places.)The p-value = (Please show your answer to 3 decimal places.)The p-value is ? α Based on this, we should Select an answer the null hypothesis.Thus, the final conclusion is that ...The data suggest the population proportion is not significantly different from 16% at α = 0.01, so there is statistically insignificant evidence to conclude that the population proportion of millionaires who can wiggle their ears is different from 16%.The data suggest the populaton proportion is significantly different from 16% at α = 0.01, so there is statistically significant evidence to conclude that the population proportion of millionaires who can wiggle their ears is different from 16%.The data suggest the population proportion is not significantly different from 16% at α = 0.01, so there is statistically significant evidence to conclude that the population proportion of millionaires who can wiggle their ears is equal to 16%.

Answer 1

We have to perform an hypothesis test on the proportion.

In this case we should use a z-test.

The claim is that the proportion of millonaires that can wiggle their ears is different from 16%.

Then, the null and alternative hypothesis are:

`\begin{gathered} H_0:\pi=0.16 \\ H_a:\pi\\e0.16 \end{gathered}`

The significance level is 0.01.

The sample has a size n = 342.

The sample proportion is p = 58/342 = 0.17.

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.16\cdot0.84)/(342)}\approx√(0.000393)\approx0.0198`

Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5\/n)/(\sigma_p)=(0.17-0.16-0.5\/342)/(0.0198)\approx(0.0085383)/(0.0198)\approx0.431`

This test is a two-tailed test, so the P-value for this test is calculated as:

`2\cdot P(z>0.431)\approx2\cdot0.333\approx0.666`

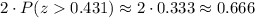
As the P-value (0.666) is greater than the significance level (0.01), the effect is not significant.

The null hypothesis failed to be rejected.

At a significance level of 0.01, there is not enough evidence to support the claim that the proportion of millonaires that can wiggle their ears is different from 16%.

Answer:

a) For this study we should use a z-test.

b) H0: p = 0.16

Ha: p ≠ 0.16

c) z = 0.431

d) p-value = 0.666

e) The p-value is greater than α.

f) Based on this we should not reject the null hypothesis.

g) The data suggest the population proportion is not significantly different from 16% at α = 0.01, so there is statistically insignificant evidence to conclude that the population proportion of millonaires who can wiggle their ears is different from 16%.