By definition, you know that when a point is rotated 90 degrees counterclockwise about the origin, point A (x, y) becomes A'(- y, x).
Then, if you rotate 90 degrees counterclockwise about the origin the points A and B you get:
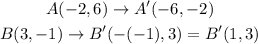
Now graphing points A and B and their respective rotations you have
Now, to know if the segments AB and A'B 'are congruent, you can find a measure of each one of them using the distance formula, which is
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
So, for the measure of segments AB you have
![\begin{gathered} (x_1,y_1)=(-2,-6) \\ (x_2,y_2)=(3,-1) \\ d_(AB)=\sqrt[]{(3-(-2))^2+(-1-(-6))^2} \\ d_(AB)=\sqrt[]{(3+2)^2+(-1+6)^2} \\ d_(AB)=\sqrt[]{(5)^2+(5)^2} \\ d_(AB)=\sqrt[]{25+25} \\ d_(AB)=\sqrt[]{50} \\ d_(AB)=7.07 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8jdm2kjfhl7pa1iprfxa6mamlrnfhict4v.png)
For the measure of segments A'B' you have
![\begin{gathered} (x_1,y_1)=(-6,-2) \\ (x_2,y_2)=(1,3) \\ d_(A^(\prime)B^(\prime))=\sqrt[]{(1-(-6))^2+(3-(-2))^2} \\ d_(A^(\prime)B^(\prime))=\sqrt[]{(1+6)^2+(3+2)^2} \\ d_(A^(\prime)B^(\prime))=\sqrt[]{(7)^2+(5)^2} \\ d_(A^(\prime)B^(\prime))=\sqrt[]{49+25} \\ d_(A^(\prime)B^(\prime))=\sqrt[]{74} \\ d_(A^(\prime)B^(\prime))=8.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mozbxoa2ow1lef198a2vurc8jtjjifnjct.png)
Then, as you can see, the segments AB and A'B'do not have the same measure and therefore are not congruent.