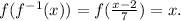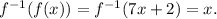Question

The function f(x)=7x+2 is one to oneFind parts A and B

Answer 1

a) To find the inverse function, first, we set the following equation:

`y=7x+2.`

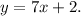
Now, we solve the above equation for x:

`\begin{gathered} y-2=7x, \\ (y-2)/(7)=x\text{.} \end{gathered}`

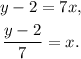
Finally, we exchange x and y

`y=(x-2)/(7),`

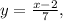
and set y=f(x). Therefore,

`f^(-1)(x)=(x-2)/(7).`

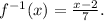
b) To verify that the above function is the inverse, we compute:

`f(f^(-1)(x))andf^(-1)(f(x)).`

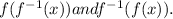
For f(f^-1(x)), we get:

`f(f^(-1)(x))=f((x-2)/(7))=7(x-2)/(7)+2=x-2+2=x.`

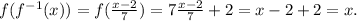
For f^-1(f(x)) we get:

`f^(-1)(f(x))=f^(-1)(7x+2)=x.`

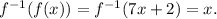
Answer:

Part A:

`f^(-1)(x)=(x-2)/(7).`

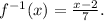
Part B:

`f(f^(-1)(x))=f((x-2)/(7))=x.`
`f^(-1)(f(x))=f^(-1)(7x+2)=x.`