Question

Number of ways to arrange the letters ELEVATED if T and D must not be next to one another.

Answer 1

Given: A collection of letters- ELEVATED.

Required: To determine the number of ways to arrange the letters ELEVATED such that T and D must not be next to one another.

Step-by-step explanation: The permutation determines the number of arrangements of the given letter. Then we can exclude the arrangements of TD and DT to get the required answer.

The total number of arrangements of given letters is-

`\begin{gathered} 8!=8*7*6*5*4*3*2*1 \\ =40320 \end{gathered}`

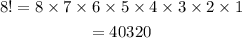
Now the total arrangements in which T and D are next to each other is-

`\begin{gathered} ^8P_2=(8!)/((8-2)!) \\ =(8*7*6!)/(6!) \\ =56 \end{gathered}`

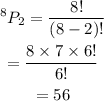
Now there can be arrangements like TD and DT. Hence we need to exclude the arrangements from the total number of arrangements as follows-

`40320-56-56=40208`

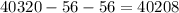
Final Answer: The number of ways to arrange the letters ELEVATED if T and D are not next to each other is 40208.