Question

8) Among middle school students, 62% play a sport, 42% play an instrument, and 34% do both. Suppose astudent selected a random and asked if they play a sport or an instrument.a)Create a Venn diagram. CONVERT THE PERCENTS TO DECIMALSb) Determine the probability that a randomly selected middleschool student plays a sport or plays an instrument.c) Determine the probability that a randomly selected middle school student plays a sport, but does not play aninstrument.d) Determine the probability that a randomly selected middle school student plays a sport, given that they play aninstrument.

Answer 1

a) From the statement of the problem, we know that among middle school students:

• 62% play a sport, 0.62 in decimals,

,

• 42% play an instrument, 0.42 in decimals,

,

• 34% do both, 0.34 in decimals.

The Venn diagram is:

b) The probability that a randomly selected middle school student plays a sport or plays an instrument is equal to the percent in decimals of the students that do both things:

`\text{Prob}=P(\text{Both)}=0.34`

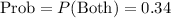
c) The probability that a randomly selected middle school student plays a sport, but does not play an instrument, is given by the part of the zone of sports without the zone of both, so the probability is:

`P(sports\&notinstrument)=0.62-0.34=0.28.`

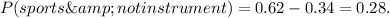
d) The probability that a randomly selected middle school student plays a sport, given that they play an instrument. Is the condition probability:

`P(A|B)=(P(A\cap B))/(P(B))\text{.}`

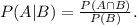
Where:

• A = a randomly selected middle school student plays a sport,

,

• B = a randomly selected middle school student plays an instrument,

,

• P(A | B) = probability of A given B,

,

• P(A ∩ B) = probability of both events = 0.34,

,

• P(B) = probability of B = 0.42.

Replacing these values in the formula above, we get:

`P(A|B)=(0.34)/(0.42)\cong0.81.`

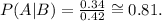
Answers

• b), 0.34

,

• c), 0.28

,

• d) ,0.81