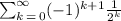Question

Write the series 1/2-1/4+1/6-1/8+... using sigma notation

Answer 1

To analyze this series, let us concentrate on the denominator of each of the fractions provided. We see that the denominators are increasing and are 2,4,6,8. All denominators are multiples of two. So, we can extend the series of numbers as below

`(1)/(2),(1)/(4),(1)/(8),....=(1)/(2^1),(1)/(2^2),(1)/(2^3),...(1)/(2^k)`

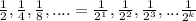
Also, see that the signs of the numbers in the series alternate, first positive then negative. We can write that like an exponential of one

`1,-1,1,-1,....=(-1)^k`

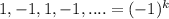
If we connect all this information, using sigma notation

`\sum_{k\mathop{=}0}^(\infty)(-1)^(k+1)(1)/(2^k)`