.
The intersection of the Lines A and B creates a pair of equivalent angles
This means
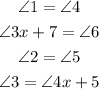
We can solve for x using the fact that the angles ∠3x + 7 and ∠3 form a linear pair. This gives us an equation and in it, we can substitute for ∠3 from the equations given above and solve the resulting equation for x.
(2).
We can solve for x using the fact that angles ∠3x + 7 and ∠3 form a linear pair. i.e .
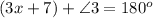
and since
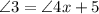
the above becomes
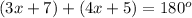
Expanding the above gives
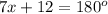
Subtracting 12 from both sides gives
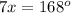
Finally, dividing both sides by 7 gives
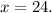
which is our answer!
(3).
Since we know that
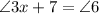
We can find the value of angle 6 by substituting the value of 3 in the above equation. This gives
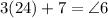
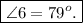
which is our answer!