Question

Let X be a random variable with the following distribution. If E(X) = 108, then x2=

Answer 1

To obtain the value of x2, the following steps are necessary:

Step 1: Recall the formula for E(X) from probability theory, as follows:

From probability theory:

`E(X)=\sum ^n_(i=1)X\cdot P(X)=X_1\cdot P(X_1)+X_2\cdot P(X_2)+\cdots+X_n\cdot P(X_n)`

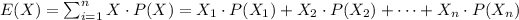
Step 2: Apply the formula to the problem at hand to obtain the value pf x2, as follows:

`\begin{gathered} \text{Given that:} \\ E(X)=108 \\ X_1=80,P(X_1)=0.3 \\ X_2=?,P(X_2)=0.7 \end{gathered}`

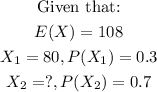
We now apply the formula, as below:

`\begin{gathered} E(X)=\sum ^2_(i=1)X\cdot P(X)=X_1\cdot P(X_1)+X_2\cdot P(X_2) \\ \text{Thus:} \\ E(X)=X_1\cdot P(X_1)+X_2\cdot P(X_2) \\ \Rightarrow108=(80)*(0.3)+X_2*(0.7) \\ \Rightarrow108=24+X_2*(0.7) \\ \Rightarrow108-24=X_2*(0.7) \\ \Rightarrow84=X_2*(0.7) \\ \Rightarrow X_2*(0.7)=84 \\ \Rightarrow X_2=(84)/((0.7))=120 \\ \Rightarrow X_2=120 \end{gathered}`

Therefore, the value of x2 is 120