Question

10. Write the equation of the graphed line. 5 4 3 N 1 -5 -4 -3 -2 -1 2 3 4 5 -2 -3 -5

Answer 1

y = -0.25x + 2

y = -¼(x) + 2

Step-by-step explanation

The slope and y-intercept form of the equation of a straight line is given as

y = mx + b

where

y = y-coordinate of a point on the line.

m = slope of the line.

x = x-coordinate of the point on the line whose y-coordinate is y.

b = y-intercept of the line.

So, we need to calculate the slope for this line.

y-intercept is the point where the line crosses the y-axis.

b = 2

For a straight line, the slope of the line can be obtained when the coordinates of two points on the line are known. If the coordinates are (x₁, y₁) and (x₂, y₂), the slope is given as

`Slope=m=\frac{Change\text{ in y}}{Change\text{ in x}}=(y_2-y_1)/(x_2-x_1)`

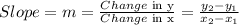
For this question, we will pick two points on it

(x₁, y₁) and (x₂, y₂) are (0, 2) and (4, 1)

`\text{Slope = }(1-2)/(4-0)=(-1)/(4)=-0.25`

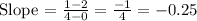
Recall that

y = mx + b

m = -0.25

b = 2

y = -0.25x + 2

Hope this Helps!!!