Question

• Create a quadratic function so that the vertex is a maximum and the range is 2,-00) and the vertex has an X-coordinate that is not 0

Answer 1

A quadratic function in vertec form is given by:

`f(x)=a(x-h)^2+k\text{ }`

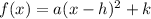
where (h,k) is the vertex of the function and a is a constant.

We know that our function has to have a maximum which means that the quadratic function has to open down; for this reason constant a has to be negative. Since we don't have enough information to determine a we choose it as -1, hence a=-1.

We also know that the range of the function is (-2,-infinity) which means that the vertex have to fullfil k=-2. The problem ask us that the x-coordinate of the vertex to be non zero hence we choose h=1.

Plugging this in the function above we have that a function that fulfills the requierements is:

`f(x)=-(x-1)^2-2`

Which has the following graph: