Question

For each equation, choose the statement that describes its solutiorIf applicable, give the solution.

Answer 1

Part A.

The equation is given by

`4(x+1)+x=3(x-2)+2`

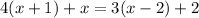
By distributing the number form into the parenthesis on the left hand side and the number 3 into the parenthesis of the right hand side, we have

`4x+4+x=3x-6+2`

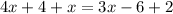
By combinig similar terms, we get

`5x+4=3x-4`

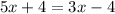
Then, by subtracting 3x to both sides, we have

`2x+4=-4`

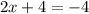
and by subtracting 4 to both sides, we get

`2x=-8`

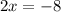
then, x is given by

`\begin{gathered} x=(-8)/(2) \\ x=-4 \end{gathered}`

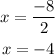
Then, the solution for part A is x=-4.

Part B

In this case, the equatiion is

`5(2+v)-v=10+4(v+1)`

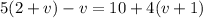
Then, by distributing the number 5 into the parenthesis and the number 4 into the parenthesis on the right hand side, we have

`10+5v-v=10+4v+4`

By combining similar terms, we have

`10+4v=14+4v`

and by subtracting 4v to both side, we have

`10=14`

which is an absurd result. Therefore, the answer for part B is. No solution