Question

How much of a 400 Gram sample of rubidium-87 would remain after 1 half life

Answer 1

200 g.

Step-by-step explanation:

What is given?

Initial quantity (N₀) = 400 g.

Half-life of rubidium-87 = 4.8 x 10¹⁰ years.

Step-by-step solution:

Let's see the formula to calculate the quantity remaining:

`N(t)=N_0\cdot((1)/(2))^{t\text{ /t}_{(1)/(2)}}.{}`

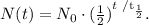
Where N₀ is the initial quantity, t is the time, and t (1/2) is the half-life of the substance, in this case, Rb-87. Based on this, our formula will be:

`N(t)=400\cdot((1)/(2))^{\text{t/\lparen4.8}\cdot10^(10))}`

If we want to find the amount of Rb-87 after 1 half-life, our t would be equal to 4.8 x 10¹⁰ years, so replacing this value in the formula we obtain:

`\begin{gathered} N(4.8\cdot10^(10))=400\cdot((1)/(2))^{4.8\cdot10^(10)\text{/4.8}\cdot10^(10)}, \\ N(4.8\cdot10^(10))=400\cdot((1)/(2))^1, \\ N(4.8\cdot10^(10))=400\cdot((1)/(2)), \\ N(4.8\cdot10^(10))=200\text{ g.} \end{gathered}`

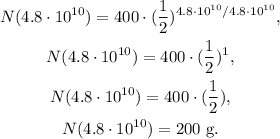
The answer is that after 1 half-life of a 400 g sample of Rb-87, the remaining quantity is 200 g.