Question

A woman at a point A on the shore of a circular lake with radius 3mi wants to arrive at the point C diametrically opposite A on the other side of the lake in the shortest possible time. She can walk at the rate of 4 mi/h and row a boat at 2 mi/h. How should she proceed

Answer 1

The distance walkin is the circumference of the semicircle:

`\begin{gathered} C=\pi\cdot r \\ \\ C=\pi\cdot3mi \\ \\ C=3\pi mi \end{gathered}`

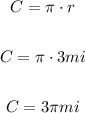
At a rate of 4 mi/h the woman will arrive at point C after 2.36 hours

`3\pi mi\cdot(1h)/(4mi)=2.36h`

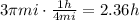
The distance in a boat is the diameter of the lake:

`\begin{gathered} d=2r \\ \\ d=2(3mi) \\ \\ d=6mi \end{gathered}`

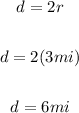
At a rate of 2 mi/h the woman will arrive at point C after 3 hours

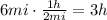
`6mi\cdot(1h)/(2mi)=3h`Then, she should go walking as the time to arrive at point C walking is 2.36 hours (shorter than the 3 hours in a boat)