ANSWER:
1st option: 6.3 min
Explanation:
Given:
Work (W) = 4.5x10^5 J
Mass (m) = 1000 kg
Height (h) = 0.8 m
Time (t) = 6 h
1 hour is equal 3600 sec, therefore:
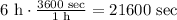
Time (t) =21600 sec
We have the following formula (Power):
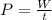
We replace the values of this case:
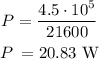
Now we calculate the work in the form of potential energy needed to lift the bricks:
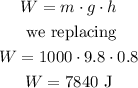
Now, we can calculate the time by calculating the ratio between the work and the power, like this:
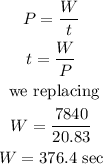
This is the time in seconds, to convert it to minutes, we must take into account that 1 minute is equal to 60 seconds, therefore:
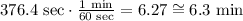
The time it would take is 6.3 minutes