Question

I need to figure out this type of 2-d momentum question, I attached the one I'm stuck on as an image.

Answer 1

Given:

The mass of the pucks, m=0.300 kg

The initial velocity of the 1st puck, u₁=3.33 m/s

The initial velocity of the 2nd puck, u₂=1.87 m/s

The final velocity of the 1st puck, v₁=2.10 m/s

To find:

The y-component of the final velocity of the 2nd puck.

Step-by-step explanation:

Let us assume that the north is the positive y-axis and the east is the positive x-axis.

As the 1st puck is going northwest, the angle made by the velocity of the 1st puck with ponegative-axis is 45 °

The velocities can be represented in the vector form as,

`\begin{gathered} \vec{u_1}=3.33cos45\degree(-\hat{i})+3.33sin45\degree\hat{j} \\ =-2.35\hat{i}+2.35\hat{j} \end{gathered}`

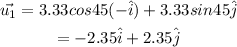
And

`\vec{u_2}=1.87(-\hat{j})=-1.87\hat{j}`

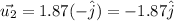
And

`\vec{v_1}=-2.10\hat{i}`

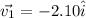
Where i-cap and j-cap are the unit vectors along the positive x and y axes respectively.

From the law of conservation of momentum, the total momentum of a system remains the same at all times. The momentum is conserved simultaneously and independently along both axes.

Considering the y-axis,

`\begin{gathered} mu_1sin45\degree\hat{j}+mu_2(-\hat{j})=0+mv_(2y)\hat{j} \\ \Rightarrow u_1sin45\degree-u_2=v_(2y) \end{gathered}`

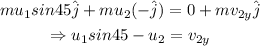
Where v_2y is the y-component of the final velocity of the second puck.

On substituting the known values,

`\begin{gathered} 3.33sin45\degree-1.87=v_(2y) \\ \Rightarrow v_(2y)=0.48\text{ m/s} \end{gathered}`

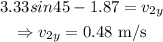
Final answer:

The y-component of the final velocity of the second puck is 0.48 m/s