The coefficient of friction μ is defined as the quotient between the force of friction f and the normal force F_N that an object is subject to:
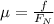
Since the friction is responsible for decelerating the car, use Newton's Second Law of Motion to find the magnitude of f:
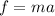
The normal force is equal to the weight of the car because the surface is horizontal:
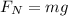
Replacing the expressions for f and F_N, the coefficient of friction becomes:
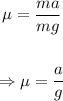
The acceleration is the rate of change of the velocity with respect to time. Since the car decelerates from 32m/s to rest in 3.94 seconds, then:
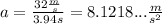
Replace the value of a as well as g=9.81m/s^2 to find the coefficient of friction:
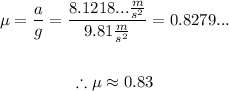
Therefore, to the nearest hundredths place, the coefficient of friction is 0.83.