Question

if the radius of a circle with an area of 12.56mm^2 is multiplied by s What is the area of the new circle?

Answer 1

The Solution.

Let the radius of the original circle be r.

By formula,

`\begin{gathered} \text{Area =}\pi r^2 \\ 12.56=3.14r^2 \\ \text{Dividing both sides by 3.14, we get} \\ r^2=(12.56)/(3.14)=4 \end{gathered}`

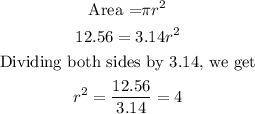
Taking the square root of both sides, we get

`r=\text{ }\sqrt[]{24}\text{ = 2mm}`

For the new circle, the radius is multiplied by 5, that is,

So, the area of the new circle is

`\begin{gathered} \text{Area =}\pi r^2=3.14*10^2 \\ \text{ =3.14}*100=314mm^2 \end{gathered}`

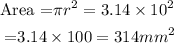
Hence, the correct answer is 314 square mm.