Answer:
t=0.64s and t=1.17s
Step-by-step explanation:
The function that models the height of the ball is given below:
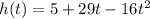
When the ball's height is 17 feet, we have:
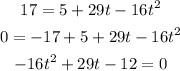
We solve the quadratic equation derived above for the values of t.
We use the quadratic formula.
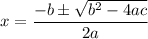
In our own equation: a=-16, b=29, c=-12
![\begin{gathered} t=\frac{-29\pm\sqrt[]{29^2-4(-16)(-12)}}{2(-16)} \\ =\frac{-29\pm\sqrt[]{841-768}}{-32} \\ =\frac{-29\pm\sqrt[]{73}}{-32} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q3tn7p3b854got0kffu736d92jl2c037db.png)
Therefore, we have:
![\begin{gathered} t=\frac{-29+\sqrt[]{73}}{-32}\text{ or }t=\frac{-29-\sqrt[]{73}}{-32} \\ t=0.6392\text{ or t=1}.1733 \\ t=0.64\text{ or t=1}.17\text{ (to the nearest hundredth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/p32ho7xx0y5h21618zyrtf3egg9qjw5uba.png)
The values of t for which the ball's height is 17 ft are 0.64 seconds and 1.17 seconds.