Question

Use the long division method to find the result when 12x3 + 27x2 + 23x + 10 is

divided by 4x + 5.

Answer 1

The division of
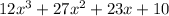`\( 12x^3 + 27x^2 + 23x + 10 \)` by
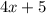`\( 4x + 5 \)` using long division results in a quotient of
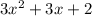`\( 3x^2 + 3x + 2 \)` and a remainder of 0. This means
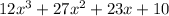`\( 12x^3 + 27x^2 + 23x + 10 \)` is exactly divisible by
`\( 4x + 5 \)`.

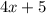1. First Step:- Divide the first term of the numerator
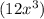`(\(12x^3\))` by the first term of the denominator
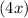`(\(4x\))`, which gives
`\(3x^2\)`.

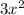- Multiply the entire denominator by
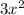`\(3x^2\)` (i.e.,
`\( (4x + 5)(3x^2) = 12x^3 + 15x^2 \)`).

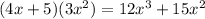- Subtract this from the original polynomial:
`\( (12x^3 + 27x^2 + 23x + 10) - (12x^3 + 15x^2) = 12x^2 + 23x + 10 \).`

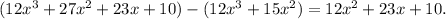
2. Second Step:

- Now, divide the first term of the new polynomial
`(\(12x^2\))` by the first term of the denominator
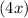`(\(4x\))`, which gives
`\(3x\)`.

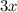- Multiply the entire denominator by
`\(3x\) (i.e., \( (4x + 5)(3x) = 12x^2 + 15x \))`.

- Subtract this from the current polynomial:
`\( (12x^2 + 23x + 10) - (12x^2 + 15x) = 8x + 10 \)`.

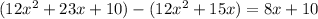3. Third Step:

- Divide the first term of the current polynomial
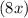`(\(8x\))` by the first term of the denominator
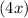`(\(4x\))`, which gives 2.

- Multiply the entire denominator by 2 (i.e.,
`\( (4x + 5)(2) = 8x + 10 \)`).

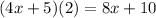- Subtract this from the current polynomial:
`\( (8x + 10) - (8x + 10) = 0 \)`.

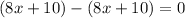Thus, the quotient is
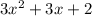`\( 3x^2 + 3x + 2 \)` and the remainder is 0.

Answer 2

12x3+27x2+23x+10/ 4x+5


3x2 + 3x + 2