The division of
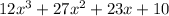 by
by
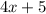 using long division results in a quotient of
using long division results in a quotient of
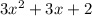 and a remainder of 0. This means
and a remainder of 0. This means
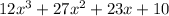 is exactly divisible by
is exactly divisible by
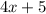 .
.
1. First Step:- Divide the first term of the numerator
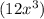 by the first term of the denominator
by the first term of the denominator
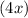 , which gives
, which gives
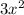 .
.
- Multiply the entire denominator by
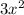 (i.e.,
(i.e.,
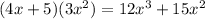 ).
).
- Subtract this from the original polynomial:
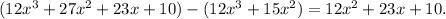
2. Second Step:
- Now, divide the first term of the new polynomial
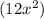 by the first term of the denominator
by the first term of the denominator
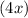 , which gives
, which gives
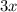 .
.
- Multiply the entire denominator by
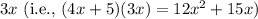 .
.
- Subtract this from the current polynomial:
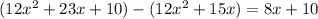 .
.
3. Third Step:
- Divide the first term of the current polynomial
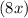 by the first term of the denominator
by the first term of the denominator
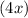 , which gives 2.
, which gives 2.
- Multiply the entire denominator by 2 (i.e.,
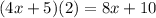 ).
).
- Subtract this from the current polynomial:
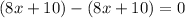 .
.
Thus, the quotient is
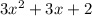 and the remainder is 0.
and the remainder is 0.