Let A be the amount of the brand of 35% pure antifreeze, and B the amount of the brand of 85% pure antifreeze.
Since a total of 70 gallons is to be obtained, then:
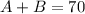
The total amount of pure antifreeze at the end should be 80% of 70, which is:
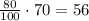
On the other hand, the total amount of antifreeze in A gallons of the first brand and B gallons of the second brand is:
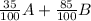
Therefore:
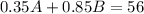
Isolate A from the first equation and substitute in the second one to find B:
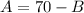

Substitute B=63 into the expression for A:

Therefore, to make a mixture of 70 gallons of 80% pure antifreeze, we need 7 gallons of the 35% pure brand and 63 gallons of the 85% pure brand.