Question

A 3.0 kg mass oscillates with a period of 0.432 seconds when attached to a spring. If the three 3.0 kg mass is removed a 1.0 kg mass is attached to the same spring, what will its new period be?

Answer 1

`\begin{equation*} 0.249\text{ seconds} \end{equation*}`

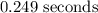
Step-by-step explanation

We want to find the period of the spring-mass system when the mass is changed.

The period of a mass-spring system is given by:

`T=2\pi\sqrt{(m)/(k)}`

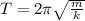
where T = period

m = mass

k = spring constant

Substitute the given values for the 3.0 kg mass:

`0.432=2\pi\sqrt{(3.0)/(k)}`

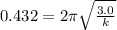
Solve for the spring constant, k:

`\begin{gathered} (0.432)/(2\pi)=\sqrt{(3.0)/(k)} \\ \\ 0.0688=\sqrt{(3.0)/(k)} \\ \\ 0.0688^2=(3.0)/(k) \\ \\ k=(3.0)/(0.0688^2) \\ \\ k=634.6\text{ kg/s}^2 \end{gathered}`

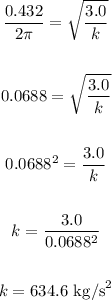
Now, solve for the period, T, when m = 1.0:

`\begin{gathered} T=2\pi\sqrt{(1.0)/(634.6)} \\ \\ T=2\pi *√(0.00158)=2\pi *0.0397 \\ \\ T=0.249\text{ seconds} \end{gathered}`

That is its new period.