You know that the center of this ellipse is at this point:

Therefore, it is centered at the Origin.
The Standard form of the equation of a ellipse centered at the Origin, is:
1. When it is horizontal:
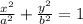
Where:
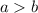
2. When it is vertical:

Where:
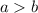
It is important to know that the coordinates of the vertices, when it is horizontal, is given by:
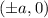
And the coordinates of the co-vertices are:
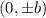
When it is vertical, the vertices are:
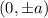
And the co-vertices:
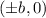
You know that, in this case, the ellipse is 10 units high and 8 units wide, then you can identify that it is vertical.
Therefore, you can find "a" and "b" as following:
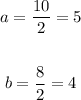
Then, its equation in Standard form is:
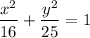
The answer is: Second option.