Question

Need help question #1. Show steps please

Answer 1

C

Explanation:

We want to integrate:

`\displaystyle \int(4x^4+3)/(4x^5+15x+2)\,dx`

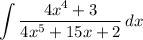
Notice that the expression in the denominator is quite similar to the expression in the numerator. So, we can try performing u-substitution. Let u be the function in the denominator. So:

`u=4x^5+15x+2`

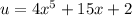
By differentiating both sides with respect to x:

`\displaystyle (du)/(dx)=20x^4+15`

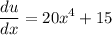
We can "multiply" both sides by dx:

`du=20x^4+15\,dx`

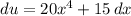
And divide both sides by 5:

`\displaystyle (1)/(5)\, du=4x^4+3\,dx`

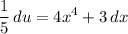
Rewriting our original integral yields:

`\displaystyle \int (1)/(4x^5+15x+2)(4x^4+3\, dx)`

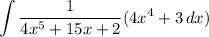
Substitute:

`\displaystyle =\int (1)/(u)\Big((1)/(5) \, du\Big)`

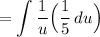
Simplify:

`\displaystyle =(1)/(5)\int (1)/(u)\, du`

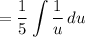
This is a common integral:

`\displaystyle =(1)/(5)\ln|u|`

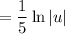
Back-substitute. Of course, we need the constant of integration:

`\displaystyle =(1)/(5)\ln|4x^5+15x+2|+C`

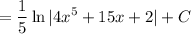
Our answer is C.